はじめに
揚力が発生するメカニズムはベルヌーイの定理より説明できます。また,この定理をもとに揚力は次の式で計算できます。
![]() ρは空気密度,Sは翼面積,vは速度,CLは揚力係数です。
揚力係数は翼の断面(翼型),面積(翼弦長 翼長),気流と主翼のなす角(迎え角),空気密度により異なるので厄介です。そこでレイノルズ数を次のように定義しています。
ρは空気密度,Sは翼面積,vは速度,CLは揚力係数です。
揚力係数は翼の断面(翼型),面積(翼弦長 翼長),気流と主翼のなす角(迎え角),空気密度により異なるので厄介です。そこでレイノルズ数を次のように定義しています。
![]() -----③
ρは空気の密度(kg/m3),vは速度(m/s),L は翼弦長(m),μ は流体の粘性係数(Pa・s)です。
レイノルズ数と迎え角の関係を測定(または計算)してそのときの速度と迎え角における揚力係数を求めます。
簡単に示すと,次の流れになります。
-----③
ρは空気の密度(kg/m3),vは速度(m/s),L は翼弦長(m),μ は流体の粘性係数(Pa・s)です。
レイノルズ数と迎え角の関係を測定(または計算)してそのときの速度と迎え角における揚力係数を求めます。
簡単に示すと,次の流れになります。
●②は翼断面の形が変わると揚力係数は異なります。 計算は大変なので「Airfoil Tools」の計算結果を用います。
ベルヌーイの定理
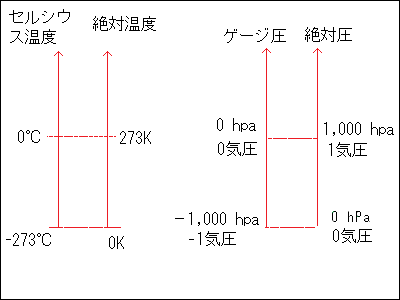
大気の圧力 気体の圧力は気体分子が当たって跳ね返ることによって生じます。したがって圧力が0と言うのは分子がない状態すなわち真空,または-237℃(絶対零度)で分子の速度が0の場合です。 工学系では,1気圧を基準にした圧力の表し方をすることがあります。これをゲージ圧といい,前者を絶対圧といいます。タイヤの空気圧などもゲージ圧です。 温度についても1気圧の下で水の凝固点を0、沸点を100とした温度(°C セルシウス温度)と分子の動きが止まる温度-273°Cを基準にした絶対温度(K ケルビン)の二つの表し方があります。(シャルルの法則で-273°Cで体積は0になります。) 圧力の単位は絶対圧もゲージ圧も同じ単位(N/m2)を使います。N/m2をpa(パスカル)とも言います。 1気圧=1.0×105 N/m2=1.0×105 pa=1,000 hPaです。 天気予報などでも真空を0として圧力を言います。もちろん物理や化学でも絶対圧が使われます。 「負圧」という言い方はゲージ圧のことで,1気圧より低いことを表しています。飛行機の翼の周りではゲージ圧で表すと正の部分や負の部分が存在します。
ベルヌーイの定理 翼の周りの空気の流れは,風洞実験で下図のようになっています。良く見る図です。
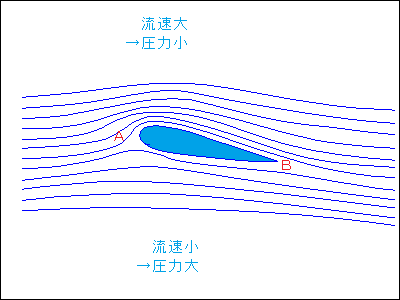 図 1
図 1
図 1 の曲線を流線といいます。同様な線に磁場のようすを表す磁束線がありますが,大きな違いがあります。それは,流線は速度ベクトルを繋いだもので磁束線は力ベクトルを繋いだものだということです。
磁束線の密度は磁場の強さを表しますが,流線の密度は速度が大きいことを表します。決して力(圧力)が大きいことを表している訳ではありません。
流線の密度が高い=速度が大きい
ベルヌーイの定理によると空気などの非圧縮性流体においては(容器に閉じ込めた気体ではないので圧縮できません)次のような関係が成り立ちます。
![]() ----①
v は気流の速さ,Pは圧力(絶対圧),ρは空気密度,P0は一定値です。
この式は気流の速さが大きいところでは圧力が低くなることを示しています。
気流の速度の速いところ(=流線の密度の高いところ)=圧力が低い
ということです。
上の図は,翼の上面の流れが下面より速いので,上面の圧力が下面より小さくなっていることを示しています。(ゲージ圧で言うと上面の圧力が負で下面が正)
したがって二つの圧力の差が揚力の原因です。これは平らな板でも翼が上下逆でも迎え角があれば同じことが起こります。
空気が静止して翼が動くのですが,相対的に考えて翼が静止していて空気が翼の速度で動くとしても同じことです。
練習用ラダー機について翼の上と下でどのくらい気流の速度に差があるか計算してみます。条件は
空気密度=1.29㎏/m3
翼弦長15㎝,翼長65㎝,翼面積0.0975m2
機体重力0.126Kg
飛行速度10.0m/s
で計算します。
機体重力から揚力は0.126kgw = 0.126×9.8= 1.23N
これを圧力に直せば翼面積0.0975m2なので
12.6N/m2
この圧力差を生み出す速度差Δvは①式より
Δv2=2×12.6÷1.29 = 19.5
∴Δv =4.4 m/s
エネルギー保存から下面の損出 = 上面の増加と考えれば
上面 10.0 + 4.4 ÷ 2 = 12.2 m/s
下面 10.0 - 4.4 ÷ 2 = 7.8 m/s
となります。
ところで今度は静止している空気中から翼を見ると翼の上下で逆の流れができています。(飛行機から見た空気の流れは相対速度です。風洞実験は飛行機からみています。こんどは地面からみます。)
----①
v は気流の速さ,Pは圧力(絶対圧),ρは空気密度,P0は一定値です。
この式は気流の速さが大きいところでは圧力が低くなることを示しています。
気流の速度の速いところ(=流線の密度の高いところ)=圧力が低い
ということです。
上の図は,翼の上面の流れが下面より速いので,上面の圧力が下面より小さくなっていることを示しています。(ゲージ圧で言うと上面の圧力が負で下面が正)
したがって二つの圧力の差が揚力の原因です。これは平らな板でも翼が上下逆でも迎え角があれば同じことが起こります。
空気が静止して翼が動くのですが,相対的に考えて翼が静止していて空気が翼の速度で動くとしても同じことです。
練習用ラダー機について翼の上と下でどのくらい気流の速度に差があるか計算してみます。条件は
空気密度=1.29㎏/m3
翼弦長15㎝,翼長65㎝,翼面積0.0975m2
機体重力0.126Kg
飛行速度10.0m/s
で計算します。
機体重力から揚力は0.126kgw = 0.126×9.8= 1.23N
これを圧力に直せば翼面積0.0975m2なので
12.6N/m2
この圧力差を生み出す速度差Δvは①式より
Δv2=2×12.6÷1.29 = 19.5
∴Δv =4.4 m/s
エネルギー保存から下面の損出 = 上面の増加と考えれば
上面 10.0 + 4.4 ÷ 2 = 12.2 m/s
下面 10.0 - 4.4 ÷ 2 = 7.8 m/s
となります。
ところで今度は静止している空気中から翼を見ると翼の上下で逆の流れができています。(飛行機から見た空気の流れは相対速度です。風洞実験は飛行機からみています。こんどは地面からみます。)
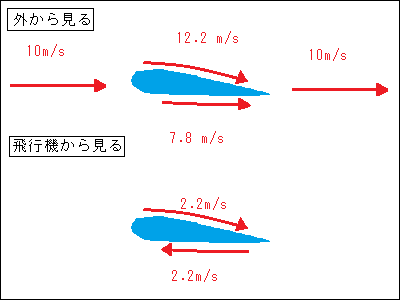
翼の周りに空気の循環ができています。翼は空気の渦を作りながら移動していきます。この渦は飛行機からみると翼端に移動し,翼端から出ていきます。(翼端渦 Wing tip vortices) 車や列車が通過したあとは空気が渦巻いているのも良く経験することだと思います。別な言い方をすれば渦ができるから揚力が発生すると言えます。
この翼端渦は抗力になりますが,揚力が発生する限りなくすことはできません。(単純に渦の中は負圧と考えていいかもしれません。翼を後方に引きます。) 翼端があるために生じる抗力です。翼端の影響をできる限り小さくするためにはアスペクト比の大きな翼(細長い翼)にする方法などがとられます。しかしこのとき翼の前面投影面積が増えるのでこれも抗力になります。
よくある勘違い よくある勘違い⑴ 「図 1 のA点で上下に分かれた気流は,B点に同時に達するから上面の流れの方が速い。」 そんなことはありません。上面の気流の方が先にB点に到達します。これは風洞実験でも明らかです。なんとなく騙されますね。 このことに関しては,ケンブリッジ大学の Holger Babinsky 教授が、風洞実験のビデオを公開されています。
ではその後はどうなるか,しばらくは渦が残っていきますが空気の粘性により時間がたてば消えていきます。上の写真からも良く分かります。 古い映画ですが,「ダイ・ハード2」(1990年のアメリカ映画)の最後あたりで旅客機が煙の中で着陸するシーンがありました。上の写真のような翼端渦が映っていました。実機で撮影したのだと思いました。
●よくある勘違い⑴ 「空気の流れの向きが水平からやや下向きに変わるので上向きに翼を押す。ベルヌーイの定理は適用できない。」 ベルヌーイの定理の各辺の単位は圧力の単位(N/m2) ですが,N=㎏m/s2として各辺にm3を掛ければ単位は ㎏(m/s)2 で,エネルギーの単位になります。簡単に言うとベルヌーイの定理はエネルギー保存の式の変形です。 エネルギー保存の式はニュートンの a=F/m から導かれるわけですから,ベルヌーイの定理から揚力を求めればよいということです。 もちろん空気の運動量の変化は翼に与える力積(こちらもa=F/m から導かれる)として計算しても同じ結果が得られるでしょう。(圧力も考慮する必要がありますが)定性的に考えるときは便利です。 「はやぶさ」が帰還したときなど,大気圏の上空で,大気が非常に稀薄で超高速の場合はボールの力積で考えることもあるかもしれません。このときは空気を非圧縮性流体として取り扱えないのです。 物理の法則には適用範囲があるのです。
レイノルズ数と揚力係数
揚力の変数 翼に働く揚力や抗力の大きさは次の量に左右されます。 ①翼の断面の形と大きさ ②翼の面積 ③機体の速度 ④機体の速度方向と翼の角度(迎え角) ⑤空気の密度 ⑥空気の粘性 このうち翼断面の長さ,機体の速度,空気の密度,粘性はレイノルズ数としてまとめます。 レイノルズ数と迎え角と揚力係数の関係を測定(または計算)して揚力を計算します。
レイノルズ数
レイノルズ数は
![]() -----③
で定義されます。
ここでρは流体の密度(kg/m3),vは流体の速度(m/s),L は長さ(m),μ は流体の粘性係数(Pa・s)です。
粘性係数は空気の場合1.83×10-5 Pa・s,空気密度は1.29㎏/m3なので,それらを代入して
Re=レイノルズ数={(速度×翼弦長)÷1.46}×105
となり,レイノルズ数は翼の長さと速度で決まります。
速度が増えるほど,翼弦長が増えるほどレイノルズ数が増えます。
模型飛行機の場合について計算すると下表のようになりました。速度の単位はm/s,翼弦長の単位はcmです。
-----③
で定義されます。
ここでρは流体の密度(kg/m3),vは流体の速度(m/s),L は長さ(m),μ は流体の粘性係数(Pa・s)です。
粘性係数は空気の場合1.83×10-5 Pa・s,空気密度は1.29㎏/m3なので,それらを代入して
Re=レイノルズ数={(速度×翼弦長)÷1.46}×105
となり,レイノルズ数は翼の長さと速度で決まります。
速度が増えるほど,翼弦長が増えるほどレイノルズ数が増えます。
模型飛行機の場合について計算すると下表のようになりました。速度の単位はm/s,翼弦長の単位はcmです。
| 速度 | 翼弦長 | レイノルズ数 | 速度 | 翼弦長 | レイノルズ数 | |
| 5 | 10 | 34,246.6 | 10 | 10 | 68,493.2 | |
| 5 | 11 | 37,671.2 | 10 | 11 | 75,342.5 | |
| 5 | 12 | 41,095.9 | 10 | 12 | 82,191.8 | |
| 5 | 13 | 44,520.5 | 10 | 13 | 89,041.1 | |
| 5 | 14 | 47,945.2 | 10 | 14 | 95,890.4 | |
| 5 | 15 | 513,69.9 | 10 | 15 | 102,739.7 | |
| 5 | 16 | 54,794.5 | 10 | 16 | 109,589.0 | |
| 5 | 17 | 58,219.2 | 10 | 17 | 116,438.4 | |
| 5 | 18 | 61,643.8 | 10 | 18 | 123,287.7 | |
| 5 | 19 | 65,068.5 | 10 | 19 | 130,137.0 | |
| 5 | 20 | 68,493.2 | 10 | 20 | 136,986.3 | |
| 5 | 21 | 71.917.8 | 10 | 21 | 143,835.6 | |
| 5 | 22 | 75,342.5 | 10 | 22 | 150,684.9 | |
| 5 | 23 | 78,767.1 | 10 | 23 | 157,534.2 | |
| 5 | 24 | 82,191.8 | 10 | 24 | 164,383.6 | |
| 5 | 25 | 85,616.4 | 10 | 25 | 171,232.9 |
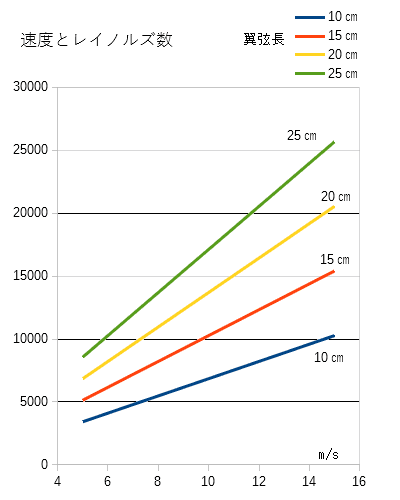
グラフ化しました。
●空気の密度や粘性係数は一定としましたが,実際は気温や湿度により空気の密度や粘性係数が変わります。どの程度変わるか計算してみました。
| 湿度 % | 空気密度 Kg/m3 | 粘性係数 Pa s | レイノルズ数 |
| 20 | 1.188 | 18.2 | 1,305,462 |
| 40 | 1.186 | 18.2 | 1,303,264 |
| 60 | 1.184 | 18.2 | 1,301,066 |
| 80 | 1.182 | 18.2 | 1,298,868 |
↑湿度80%のときのレイノルズは20%のときの99.4%なのでほとんど誤差範囲です。
| 温度℃ | 空気密度 Kg/m3 | 粘性係数 Pa s | レイノルズ数 |
| 5 | 1.253 | 17.5 | 1,424,241 |
| 10 | 1.230 | 17.7 | 1,388,473 |
| 20 | 1.186 | 18.2 | 1,303,264 |
| 25 | 1.165 | 18.4 | 1,263,624 |
↑温度25℃のときのレイノルズは5℃のときの89%です。
湿度が上がると空気密度は小さくなります。したがってレイノルズ数は小さくなります。これは窒素(分子量28),酸素(32)の代わりに水蒸気(18)に置き換わるからです。(同温同圧で同体積の分子数は変わりません。)この密度の変化の影響はほとんどありません。 気温が上がると気体は体積が増えるので空気密度は下がり,粘性係数は増えますが,空気密度の影響がレイノルズ数には大きく寄与します。 気温の低い方が飛ばしやすいと言えます。
レイノルズ数と揚力係数 揚力係数はレイノルズ数と迎え角により下図のように変化します。
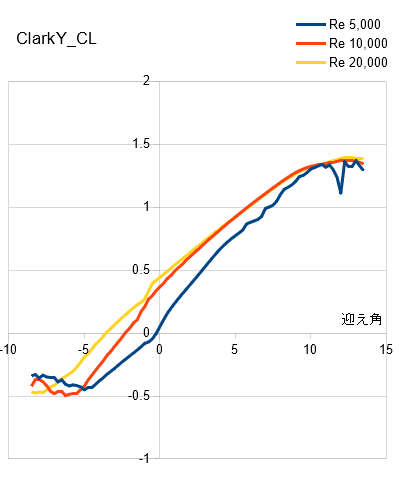
↑「Airfoil Tools」のデータより
揚力係数は実験により測定するかコンピューターを用いて計算するしかありません。幸いにも模型飛行機の大きさの翼に対して,コンピューターを用いて計算した結果を豊富に掲載しているサイト「Airfoil Tools」があります。ここにあるデータ利用すれば揚力が計算できます。 ●「翼型の比較と断面図の作製」のページに模型飛行機でよく使われる翼型のデータをグラフ化したものを掲載しています。参照してください。
揚力・抗力計算
揚力の計算式
レイノルズ数が分かり,揚力係数が分かれば揚力は 簡単に計算できます。
揚力(Lift)は次のように計算できます。
![]() -----②
ρは空気密度,Sは翼面積,vは速度,CLは揚力係数です。
模型飛行機に限定し,空気密度を1.29㎏/m3,翼面積の単位を㎝2,揚力の単位をgf,速度の単位をm/sとすれば
L = 0.0645 × 速度2 × 翼面積 × 揚力係数(gf)-----②'
と簡単に書けます。
この揚力係数が曲者で,翼の長さと速度,レイノルズ数によって変わってきます。
(この式は翼の廻りの循環を利用してクッタ・ジューコフスキーの定理から導き出されます。)
●翼弦長が決まれば速度の変化によるレイノルズ数は簡単に計算できますが,揚力係数はレイノルズ数と迎え角により変化します。この揚力計数を求めるには実測するかコンピューターで計算する以外に方法がありません。
上のグラフをもとに特定の翼弦長,速度による揚力は計算できますが,迎え角10°あたりで揚力が最大と理解しておけば充分です。
また,揚力とともに抗力も増えます。
●揚力係数が最大になるときの迎え角を失速迎え角といいます。それ以降の状態は失速です。(空気の流れが剥離します。)失速迎え角のとき,抗力は急激に大きくなります。
揚力係数の最大値で飛ぶことは危険で,ありえません。
飛行機が滑空するときの最低速度は最大揚力係数とは関係ありません。取り付け角度をもとに滑空の最低速度を求めます。
-----②
ρは空気密度,Sは翼面積,vは速度,CLは揚力係数です。
模型飛行機に限定し,空気密度を1.29㎏/m3,翼面積の単位を㎝2,揚力の単位をgf,速度の単位をm/sとすれば
L = 0.0645 × 速度2 × 翼面積 × 揚力係数(gf)-----②'
と簡単に書けます。
この揚力係数が曲者で,翼の長さと速度,レイノルズ数によって変わってきます。
(この式は翼の廻りの循環を利用してクッタ・ジューコフスキーの定理から導き出されます。)
●翼弦長が決まれば速度の変化によるレイノルズ数は簡単に計算できますが,揚力係数はレイノルズ数と迎え角により変化します。この揚力計数を求めるには実測するかコンピューターで計算する以外に方法がありません。
上のグラフをもとに特定の翼弦長,速度による揚力は計算できますが,迎え角10°あたりで揚力が最大と理解しておけば充分です。
また,揚力とともに抗力も増えます。
●揚力係数が最大になるときの迎え角を失速迎え角といいます。それ以降の状態は失速です。(空気の流れが剥離します。)失速迎え角のとき,抗力は急激に大きくなります。
揚力係数の最大値で飛ぶことは危険で,ありえません。
飛行機が滑空するときの最低速度は最大揚力係数とは関係ありません。取り付け角度をもとに滑空の最低速度を求めます。
揚力計算 翼弦長は飛行中変化しないので,「速度が増えると揚力係数は増加する」ということになります。 従って同じ機体で,例えばバッテリーを大きくしたり,カメラを搭載したりしたときは揚力を増やすために速い速度で飛行させる必要があります。 速度が同じとき,翼弦長が大きくなれば揚力係数も大きくなるので,同じ翼面積ならば翼弦長の大きい方が有利となります。 ただし,翼弦長を増やしただけでは安定性が悪くなります。 練習用ラダー機の場合,水平尾翼容積比と垂直尾翼容積比は次のように変わります。
| 翼弦長 | 翼長 | 容積比 | |
| 水平尾翼 | 垂直尾翼 | ||
| 15 | 65 | 0.44 | 0.055 |
| 20 | 49 | 0.33 | 0.073 |
●模型飛行機の場合,垂直尾翼容積比は0.02~0.05,水平尾翼容積比は0.30~0.60程度と思われます。 数値が大きいほど安定ですが,安定しすぎるとこんどは操縦できません。(曲がろうとしても曲がれなくなります。) ●データは「Airfoil Tools」のデータを利用しています。
次に揚力係数が分かったので②式を利用して揚力を計算してみます。条件は練習用ラダー機を想定しています。 翼長60㎝,翼弦長15㎝,翌面積 900㎝2 空気密度 1.29㎏/m3 迎え角0°と1°,2°について計算しています。(水平飛行を想定しています。)
| 速度 | レイノ ルズ数 | 迎え角 0° | 迎え角 1° | 迎え角 2° | ||||
| m/s | Km/s | 揚力係数 | 揚力gf | 揚力係数 | 揚力gf | 揚力係数 | 揚力gf | |
| 2 | 7.2 | 20,548 | 0.095 | 22 | 0.153 | 34 | ||
| 3 | 10.8 | 30,822 | 0.143 | 75 | 0.230 | 114 | ||
| 4 | 14.4 | 41,096 | 0.191 | 177 | 0.307 | 270 | ||
| 5 | 18.0 | 51,370 | 0.051 | 73 | 0.239 | 346 | 0.383 | 556 |
| 6 | 21.6 | 61,644 | ||||||
| 7 | 25.2 | 71,918 | ||||||
| 8 | 28.8 | 82,192 | ||||||
| 9 | 32.4 | 92,466 | ||||||
| 10 | 36.0 | 102,740 | 0.367 | 2133 | 0.495 | 2873 | 0.609 | 3532 |
| 11 | 39.6 | 113,014 | ||||||
| 12 | 43.2 | 123,288 | ||||||
| 13 | 46.8 | 133,562 | ||||||
| 14 | 50.4 | 143,836 | ||||||
| 15 | 54.0 | 154,110 | ||||||
| 16 | 57.6 | 164,384 | ||||||
| 17 | 61.2 | 174,658 | ||||||
| 18 | 64.8 | 184,932 | ||||||
| 19 | 68.4 | 195,205 | ||||||
| 20 | 72.0 | 205,479 | 0.442 | 10273 | 0.542 | 12583 | 0.640 | 14865 |
データが少なくて大雑把なことしか言えませんが。上の「レイノルズ数の違いによる揚力係数と迎え角の関係」のグラフで,ある迎え角におけるレイノルズ数と揚力係数の関係は「Airfoil Tools」には3点しかデータがありません。(表の青い部分です。オレンジ色部分は類推です。) 速度が2倍になれば揚力は4倍ではありません。なぜなら 速度が増えると → レイノルズ数が増える → 揚力係数が増える となるので揚力は4倍以上になります。 10m/s(36.0Km/s)のとき迎え角1°で"揚力2,873gfは大きすぎる気がします。5m/s(18.0Km/s)のとき迎え角1°で346gfはそんなものかなと思います。 5m/sで飛ぶときの揚力が383gfですから,機体重量が150gならば水平飛行するときの(揚力=重力)の時の速度はそれ以下です。表の赤い部分は揚力係数が一様に減少したときの推定値です。練習用ラダー機はこの付近の速度で飛行します。データがなくて残念です。 もちろんエレベーターダウンで頭を押さえて(風圧中心が前に移動するので)5m/sあるいはそれ以上の速度で水平飛行させることはできます。 20m/s(72.0Km/s)のときも計算して見ましたが練習用ラダー機ではありえない速度です。 模型飛行機に対しての揚力係数は傾向をつかむだけで正確に計算するのは無理なようです。
抗力係数と抗力計算
一般的に抗力も
![]() ------④
のように書かれます。Cdは抵抗係数,ρは空気密度,Sは前面投影面積,vは速度で表されますが,Cdを減らすために良く用いられるのが流線形です。
翼型による抗力係数CDの違いは次のようになります。
------④
のように書かれます。Cdは抵抗係数,ρは空気密度,Sは前面投影面積,vは速度で表されますが,Cdを減らすために良く用いられるのが流線形です。
翼型による抗力係数CDの違いは次のようになります。
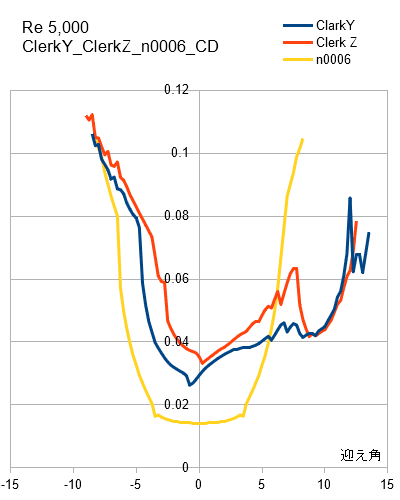
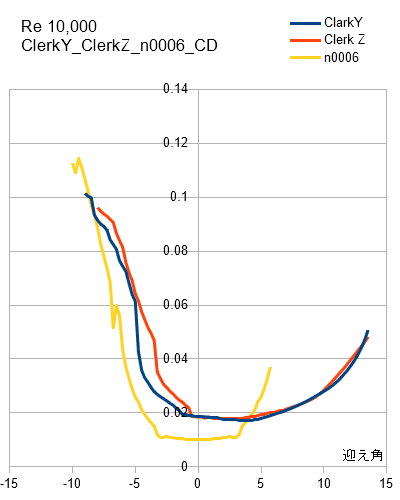
揚抗比 次の図は揚抗比(CL/CD)です。 揚抗比が大きい(揚力>抗力)ということは少ない推力で飛行できるということになり,揚抗比が最大になる迎え角での飛行が最も経済的となります。ただし,二つのグラフを比較すると分かりますが失速直前の迎え角です。
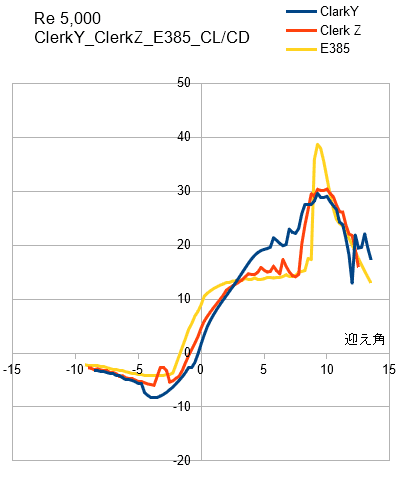
クラークYについて,抗力係数は迎え角0~10°の範囲ではあまり変化しません。ただし,抗力の計算も揚力と同様の計算なので抗力は速度が増えれば当然増えます。 抗力係数から判断して,迎え角10°付近を超えると急激に抵抗が増えると理解しておけば充分と思います。 迎え角0~10°の範囲では,抗力係数は増えずに揚力係数が増えます。最大揚力係数ときの角度を失速角と言い,この角度を超えると抗力が急激に増え,失速します。 クラークYは扱いやすく模型飛行機に適した翼型だと思います。クラークZもクラークYに近い特性ですが,E385は癖があり,性能を引き出すのは難しいように思います。 ●矩形翼以外のテーパー翼などは場所により翼弦長が異なるのでレイノルズ数が異なり揚力計数が異なります。そのような場合は,模型では平均翼弦長で計算すれば十分と思います。 ●データは「▶Airfoil Tools」のデータを利用しています。
迎え角 迎え角は気流に対する角度です。 迎え角0~10°の間で飛行させることが必要ですが,ここで迎え角とは気流に対する角度ですから例えば水平と30°で上昇中でも迎え角は0~10°にできます。 上昇中は抗力と重力の飛行方向と逆向きの成分がありますから水平飛行中より大きな推力を必要とします。
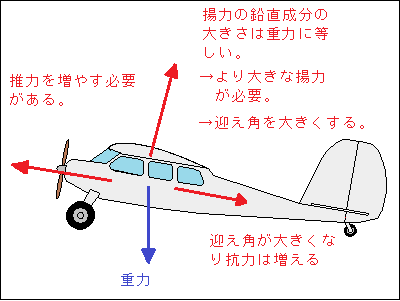
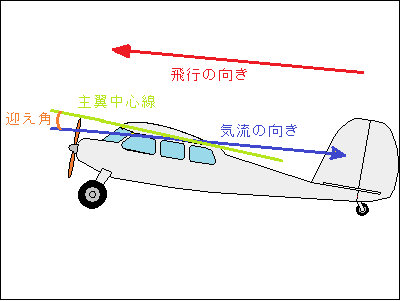
レイノルズ数が小さい小型の模型飛行機の場合,同じ翼面積で考えると翼長を短くして翼弦長を長くすればレイノルズが大きくなり,揚力係数は大きくなることは予測できますが,翼弦長は水尾翼容積比,垂直尾翼容積比にも影響しますから注意が必要です。
翼型と誘導抗力・失速
e01翼端渦と誘導抗力 翼の平面形により失速時の特性や翼端に発生する渦による誘導抗力が異なってきます。無限長の翼は存在しないのでどうしても翼端による誘導抗力が発生します。 ここでは主な翼平面の特徴を示します。
e02矩形翼 長方形の翼。翼の付け根付近から失速するのでエルロンが最後まで効き操縦しやすい。 リブがすべて同じサイズで作りやすい。
↑Original image:
▶
aeroprints.com
Original image:▶via Wikimedia Commons
Copyright:[CC BY-SA 3.0]
e03楕円翼 楕円形の翼。翼端渦による誘導抗力が小さい。作成が面倒で実機でも現在はほとんど採用されない。第二次世界大戦の飛行機に多い。 誘導抗力の計算には楕円からどれだけずれるかを計算につかいます。楕円のときが誘導抗力は最小です。
e04テーパー翼 台形の翼。翼端から失速する。リブのすべてサイズが異なり作るのが面倒。 翼端失速を避けるために翼を「捩り下げ(捻り下げ)」します。零戦の「捻り下げ」が有名です。
テーパー翼は端に行くほど翼弦長が短くなり,同じ速度でも翼端のレイノルズ数は小さくなります。レイノルズ数が小さい翼は失速角度が小さくなるので迎え角が大きくなっていくとき先に翼端が失速することになります。それを防ぐために翼端を2~3°下向きにします。 ラジコン飛行機は失速角近くで飛ばすことはあまりなく,2~3°の角度の違いは目視できないしコントロールもできないと思います。下げすぎて全体の揚力を減らすより何もしない方がよいのではないかと思います。
翼面荷重と最低速度
前出の揚力の式ですが,(②式)
水平飛行時の揚力は最低機体の重さでよいと考えられます。
すると左辺のLを機体の重さとし,これをvについて解けば
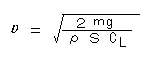 これが水平飛行時の最低速度となります。
CL(揚力係数)はレイノルズ数(速度,翼弦長)と迎え角によりますが,水平飛行なので迎え角は一定です。しかし,右辺にも速度が含まれるので「最低速度は飛行機の質量の平方根に比例する」とは言えないことになります。
速度が増えればレイノルズ数が増えますから揚力係数も増えます。したがって飛行機の質量が2倍になったとき,最低速度は1.4倍ではなく,それよりも小さくなります。(クラークYで1.3倍程度と類推されます。)
上式で,
これが水平飛行時の最低速度となります。
CL(揚力係数)はレイノルズ数(速度,翼弦長)と迎え角によりますが,水平飛行なので迎え角は一定です。しかし,右辺にも速度が含まれるので「最低速度は飛行機の質量の平方根に比例する」とは言えないことになります。
速度が増えればレイノルズ数が増えますから揚力係数も増えます。したがって飛行機の質量が2倍になったとき,最低速度は1.4倍ではなく,それよりも小さくなります。(クラークYで1.3倍程度と類推されます。)
上式で,
![]() を翼面荷重(g/dm2)と言います。翼面荷重と揚力係数を用いて次のようにも書けます。
を翼面荷重(g/dm2)と言います。翼面荷重と揚力係数を用いて次のようにも書けます。
 翼面荷重をA(単位 g/dm2),揚力係数をCLとすれば最低速度は
翼面荷重をA(単位 g/dm2),揚力係数をCLとすれば最低速度は
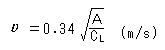 このように翼面荷重と揚力係数が分かれば最低速度の計算は簡単です。
仮に揚力係数を0.2とすれば次のようになります。
このように翼面荷重と揚力係数が分かれば最低速度の計算は簡単です。
仮に揚力係数を0.2とすれば次のようになります。
| 翼面荷重 | 最低速度 |
| 50 g/dm2 | 5.4 m/s |
| 40 g/dm2 | 4.8 m/s |
| 30 g/dm2 | 4.2 m/s |
| 20 g/dm2 | 3.4 m/s |
| 10 g/dm2 | 2.4 m/s |
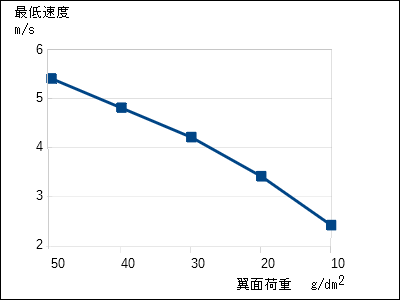
●揚力係数は速度や翼弦長,迎え角,翼型により異なります。迎え角1~2°で滑空していると仮定しました。一応の目安です。 ●最大揚力係数はおよそ10°~15°です。このような迎え角では滑空しません。これより小さい角度で抗力が急激に増加します。失速直前です。 同じ翼面積でも重い機体は翼面荷重が大きくなります。最低飛行速度は機体重量の平方に比例しますから,バッテリーを重いものに変えたり,補強で重くなったりすると飛行最低速度は大きくなってしまいます。ゆっくり飛ぶ機体を作るには翼面荷重を小さくして機体重量を抑えることが必要です。 練習用ラダー機は全重量 126.5 g 翼面荷重 13.0 g/dm2なのでゆっくり飛ばせます。
●模型飛行機については 翼型は癖のないクラークYで十分 揚力の計算など必要ない。翼面荷重の計算で十分 翼面荷重は15~40程度の範囲にする。 と考えます。
主翼取り付け角
揚力係数の測定値の迎え角0°は前縁と後縁を結んだ下図の基準線(赤)です。翼弦の下を機体の中心線に合わせると取り付け角度がつくことになります。これは翼型により異なります。機体に取り付けるときは注意が必要です。
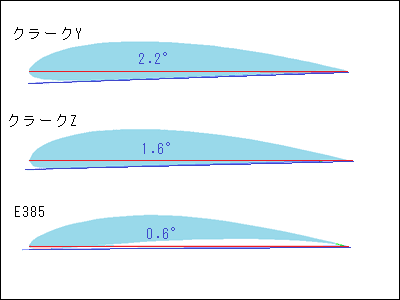
主翼取り付け角度を大きくすると揚力が増えて低速では良く滑空しますが,パワーハイで上昇し過ぎる。(頭上げになる) またうっかりするとハイパワー時に迎え角が大きくなりすぎ失速します。このときの失速はスティクニュートラルでこの後頭下げになるのでリカバリーしやすい。 実機より取り付け角を少なくした方が飛ばし易いことが多い。 これは実機に対してラジコン飛行機はオーバーパワーであることが多いためと考えます。 主翼取り付け角度を小さくして滑空性能を落とすか,スロットルとエレベーターを連動させて頭上げを防ぐか微妙です。 次の図は翼長100㎝,翼弦長20㎝のクラーク Y について迎え角0°と2°について,揚力を計算して見ました。
| レイノ ルズ数 | 迎え角 ° | 揚力係数 | 速度 m/s | 速度 Km/h | 揚力 Kgf |
| 50,000 | 0 | 0.0506 | 3.6 | 13.1 | 0.083 |
| 2 | 0.3833 | 0.625 | |||
| 100,000 | 0 | 0.3674 | 7.3 | 26.3 | 2.397 |
| 2 | 0.6085 | 3.969 | |||
| 200,000 | 0 | 0.4424 | 14.6 | 52.5 | 11.539 |
| 2 | 0.6402 | 16.659 |
迎え角0°では速度が遅いとき揚力は不足すると思われます。ただし,クラーク Y は後70% がフラットなのでこの部分を機体中心軸に平行にすれば,取り付け角度は約2.2°になります。 ●翼型については「▶CUIUC Airfoil Data Site」のサイトに揃っています。gifファイルと座標データがあります。揚力係数の値については「▶Airfoil Tools」のデータを使いました。
「Airfoil Tools」の使い方
▶「Airfoil Tools」のサイトに「UIUC Airfoil Data Site」の翼型座標を使って計算した揚力係数など豊富なデータがあります。 ここのデータから揚力が計算できます。模型飛行機に特化しています。
「Download as CSV file:」をクリックすればCSVファイル(数値データ)のダウンロードできます。Excelに貼り付けてレイノルズ数の違いによる比較グラフを簡単に作れます。
csvの項目と意味は次のようになっています。
①Alpha
迎え角
②CL
揚力係数
![]() ③Cd
抗力係数
③Cd
抗力係数
![]() ④Cdp
④Cdp
![]() 全抵抗係数Cdの内の翼型抵抗係数(たぶん?)
面積Sは翼の全面投影
全抵抗係数Cdの内の翼型抵抗係数(たぶん?)
面積Sは翼の全面投影
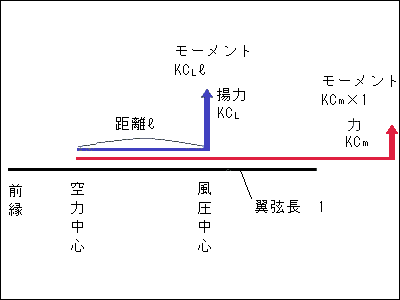
⑤Cm
モーメント係数
揚力が持つ空力中心の周りのモーメント。腕の長さは翼弦長です。
力=揚力 × 係数
モーメント=揚力 × 係数 × 翼弦長
翼弦長を1とし,揚力を,定数kを用いてkCLとすればモーメントはkCm × 1 となる。
揚力のモーメントは腕の長さ(空力中心から風圧中心までの距離)をℓとすればkCL×ℓ
両方のモーメントが等しいので
![]() これを翼の前縁から測れば
これを翼の前縁から測れば
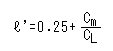 翼弦長を1としたので ℓ'は前縁からの百分率になります。
なお,モーメントには正負があるので注意が必要です。
翼弦長を1としたので ℓ'は前縁からの百分率になります。
なお,モーメントには正負があるので注意が必要です。
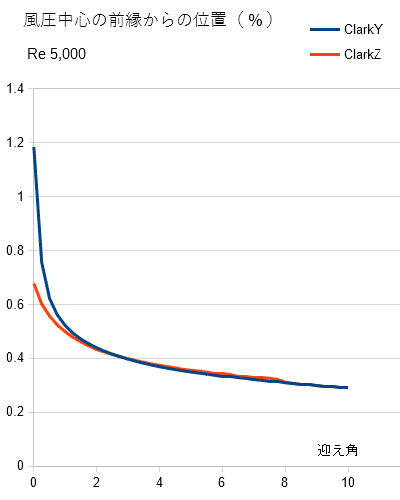
⑥Top_Xtr 層流から乱流への強制遷移の位置 ⑦Bot_Xtr 層流から乱流への強制遷移の位置 ※ ② ÷ ③で揚抗比が計算できます。 ※ 縦軸②横軸②でグラフを書けばポーラーカーブが簡単にできます。 ●Ncritについて Ncritが5と9が選択できるようになっていますが,Ncritは翼型解析ソフトxfoilのパラメーターで空気の乱れの程度です。小さいほど乱れていることになります。 xfoilは翼型上の圧力分布を計算し,与えられた翼型の揚力および抗力を求めるソフトです。 現在は模型飛行機の設計に使用されるソフトXFLR5に統合されています。 ●「Airfoil Tools」のデータは「Xfoil」による解析結果です。「Xfoil」は模型飛行機用のフリーの2次元翼型解析ソフトでMITのMark Drela教授の開発です。ちょっと使いにくいのと計算に時間がかかるのでここのデータを見たほうが便利です。
参考文献等 ▶www.cfijapan.com 揚力・抗力係数データ ▶Airfoil Tools ●「よくわかる航空力学の基本」 東京都立産業技術高等専門学校教授 飯野明 監修 ▶西脇技術士事務所 翼座標データ ▶UIUC Airfoil Data Site 科学技術計算 ▶科学技術計算ツール